Architecture
Résolution par la méthode des éléments finis
Dans la troisème partie de ce projet, nous implémentons classes et fonctions dans le but de résoudre l'équation de Poisson en 2D sur un maillage triangulaire en utilisant la méthode des éléments finis.
Pour résoudre l'équation de Poisson par la méthode des éléments finis, nous devons assembler les matrices élémentaires A_K et F_K pour chaque triangle K du maillage.
Les éléments de ces matrices sont des intégrales de produits de fonctions.
Classes heritées de Evaluator
Plusieurs classes héritées de Evaluator ont été implémentées dans le but de calculer l'évaluation de plusieurs type de fonctions.
EvaluatorConst(double c)qui permet de calculer l'évaluation d'une constantec.EvaluatorProduct(const Evaluator &e1, const Evaluator &e2)qui permet de calculer l'évaluation du produit de deuxEvaluators.EvaluatorPhiK(Node **n, int k, Element *e)qui permet de calculer l'évaluation de la fonction de formephi_kde l'élémente.
Fonctions formes
La fonction double Element::phi_k(Node **nodes, int k, double x, double y) calcule la fonction de forme phi_k de l'élément e au point (x, y).
La fonction tuple<double, double> Element::grad_phi_k(Node **nodes, int k) const calcule le gradient de la fonction de forme phi_k de l'élément e. Cette fonction renvoie un std::tuple contenant les deux composantes du gradient.
Veuillez noter que cette fonction ne prend pas d'arguments x et y car le gradient d'une fonction de forme est indépendant de la position (x, y).
En effet, les gradients des fonctions de formes sont les vecteurs constants suivants:
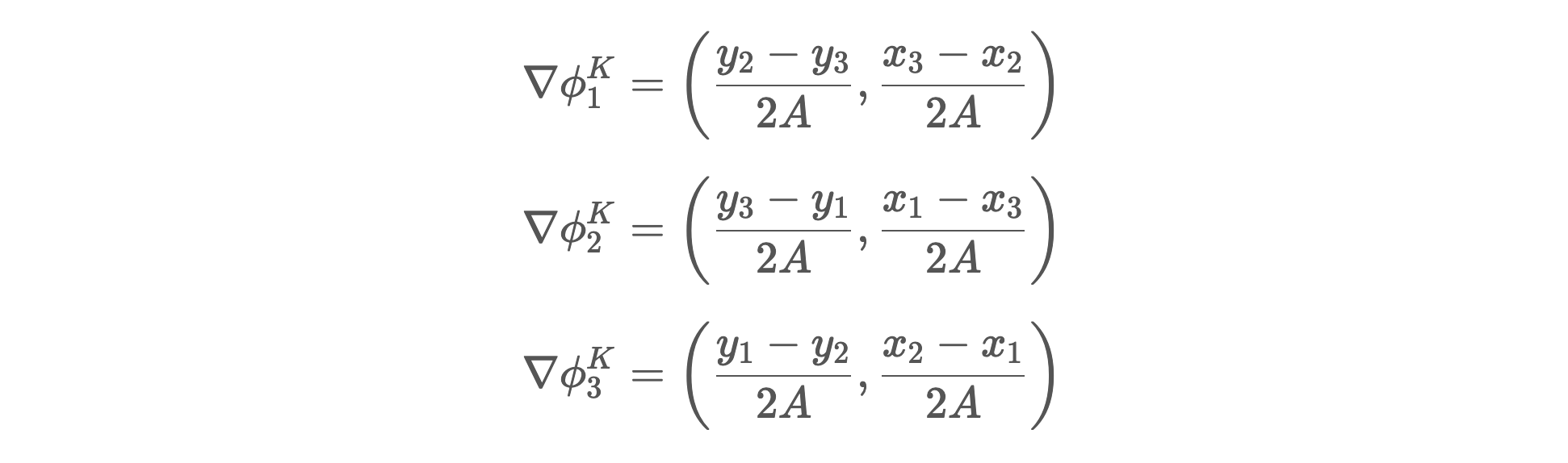
avec A, l'aire de l'élément K.
Matrices élémentaires
Une méthode Eigen::MatrixXd AKe(Node **nodes, int quad_order) a été implémentée dans la classe Element pour calculer la matrice élémentaire A_K de l'élément e pour un ordre de quadrature quad_order.
Elle retourne une matrice Eigen::MatrixXd de taille 3x3.
Pour chaque élément de la matrice, le produit scalaire entre le gradient de deux fonctions de forme est calculé.
Ce produit scalaire (une constante) est ensuite intégré sur l'élément K en utilisant la fonction integral de l'élément à l'aide de EvaluatorConst.
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
std::tuple<double, double> grad_phi_i = this->grad_phi_k(nodes, i + 1);
std::tuple<double, double> grad_phi_j = this->grad_phi_k(nodes, j + 1);
double res = std::get<0>(grad_phi_i) * std::get<0>(grad_phi_j) + std::get<1>(grad_phi_i) * std::get<1>(grad_phi_j);
EvaluatorConst eval(res);
AK(i, j) = this->integral(quad_order, eval, nodes);
}
}
Vecteurs élémentaires
Une méthode Eigen::VectorXd FKe(Node **nodes, Evaluator const &eval_f, int quad_order) a été implémentée dans la classe Element pour calculer le vecteur élémentaire F_K de l'élément e pour un ordre de quadrature quad_order.
Elle retourne un vecteur Eigen::VectorXd de taille 3.
Pour chaque élément du vecteur, eval_phi_k est défini pour calculer la fonction de forme phi_k de l'élément e et EvaluatorProduct est défini pour calculer le produit de eval_f et eval_phi_k.
Ce produit est ensuite intégré sur l'élément K.
for (int i = 0; i < 3; i++)
{
EvaluatorPhiK eval_phi_k(nodes, i + 1, this);
EvaluatorProduct eval_g(eval_f, eval_phi_k);
FK(i) = this->integral(quad_order, eval_g, nodes);
}
Algorithme d'assemblage
La classe FiniteElement permet de résoudre le problème de Poisson par la méthode des éléments finis sur un maillage Mesh spécifié au contructeur.
La fonction Eigen::VectorXd FiniteElement::solve(Evaluator const &eval_f, Evaluator const &eval_g, int quad_order) prend en argument les évaluateurs eval_f et eval_g de la fonction f et de la fonction g, ainsi que l'ordre de quadrature quad_order.
Des matrices creuses typedef Eigen::SparseMatrix<double, Eigen::RowMajor> sparse_matrix_type sont utilisées pour stocker les matrices A et F du système linéaire AU = F.
Il s'agit dans un premier temps de contruire la matrice A et le vecteur F du système linéaire AU = F. La matrice A étant creuse, on utilise un std::vector<Eigen::Triplet<double>> pour stocker l'association (i, j, a_ij) des éléments non nuls de la matrice A.
On construit ensuite cette matrice A à partir de ce vecteur.
A.setFromTriplets(tripletList.begin(), tripletList.end());
On utilise par la suite la méthode d'élimination sur les noeuds au bord du maillage :
std::set<int> rows;
for (int i = 0; i < M_mesh->nb_edges(); i++)
{
int edge = M_mesh->edge(i);
rows.insert(edge);
double xi = M_mesh->node(edge)->x();
double yi = M_mesh->node(edge)->y();
F(i) = eval_g(xi, yi);
}
for (int rowId : rows)
{
for (typename sparse_matrix_type::InnerIterator it(A, rowId); it; ++it)
{
if (it.row() == it.col())
{
it.valueRef() = 1.0;
}
else
{
it.valueRef() = 0;
}
}
}
On résout enfin le système linéaire grâce à Eigen pour obtenir la solution approchée sol :
Eigen::SparseLU<sparse_matrix_type> solver;
solver.analyzePattern(A);
solver.factorize(A);
Eigen::VectorXd sol = solver.solve(F);
Export de la solution
La fonction void export_vtk_vector(Mesh &mesh, Eigen::VectorXd sol, std::string file_name) est identique à la fonction export_vtk de la partie 2, à l'exception près que le vecteur sol est utilisé pour définir les valeurs de la solution aux noeuds du maillage.
for (int i = 0; i < mesh.nb_nodes(); i++)
ofile << sol(i) << std::endl;
Tests
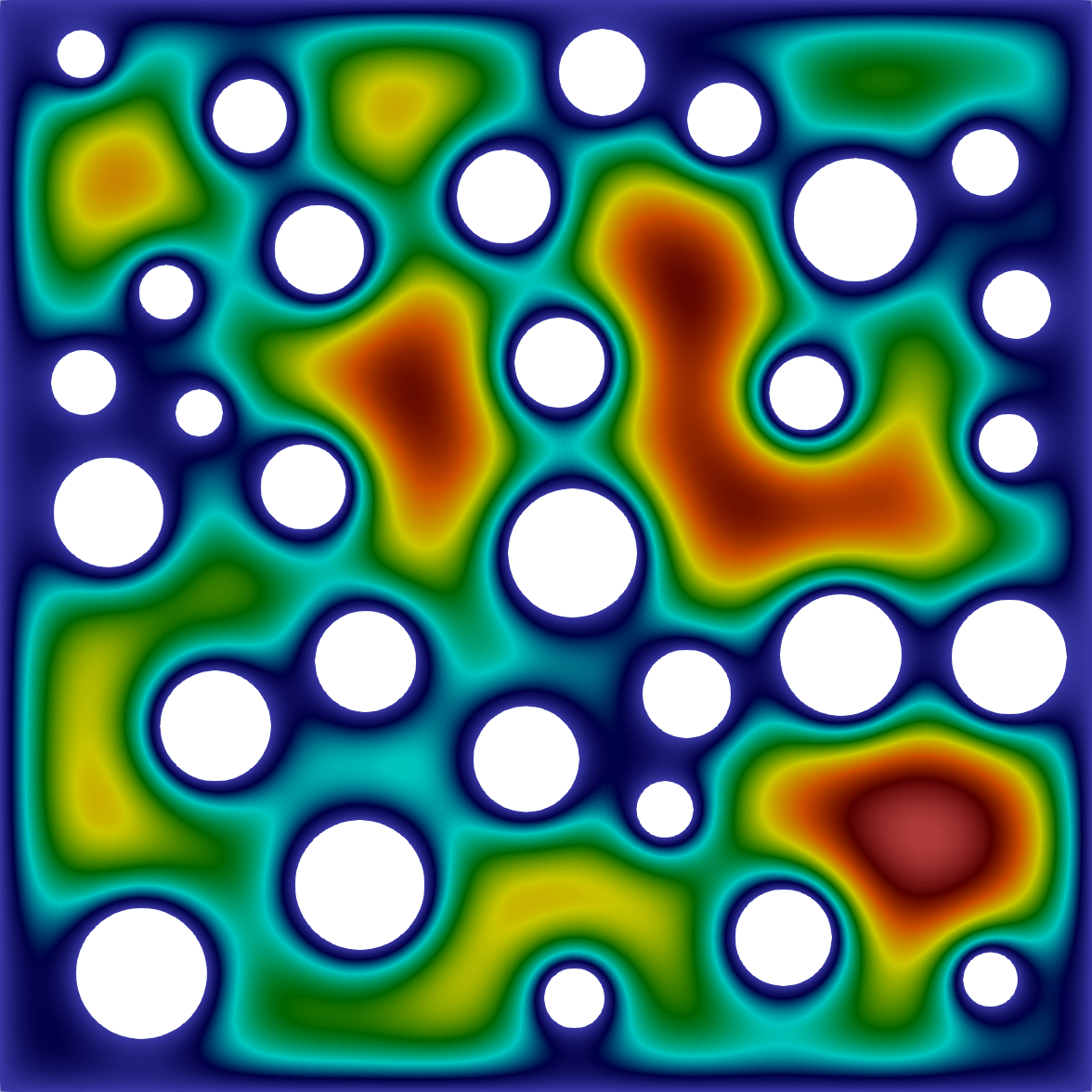
Le fichier tests/part_3.cpp contient le code générant les figures de l'énoncé, à savoir la résolution de l'équation de Poisson en 2D suivante :
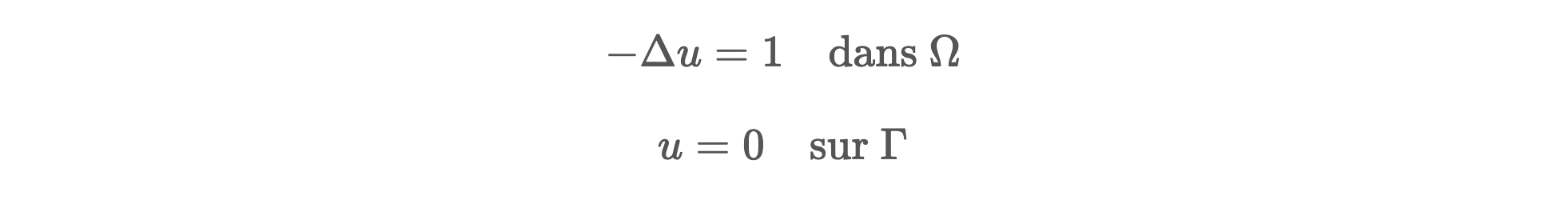
sur le maillage mesh_M2 :

ainsi que sur le maillage mesh_perforated :