Architecture
Post-traitements
Dans la deuxième partie du projet, nous créons un programme permettant de visualiser une expression sur un maillage et de calculer des intégrales sur ce maillage.
Visualisation d'une expression
Pour visualiser une expression f, il est nécéssaire d'itérer sur les noeuds du maillage et d'évaluer la fonction sur chaque noeud. Un fichier .vtk est ensuite généré en sortie pour être visualisé avec Paraview.
Une fonction void export_vtk(Mesh &mesh, Evaluator const &eval_f, std::string file_name) a été créee dans ce but. Cette fonction prend en paramètre un pointeur sur un maillage, un pointeur sur un évaluateur de fonction et le nom du fichier de sortie.
Comme indiqué dans la partie précédente, des opérateurs de sortie pour les différents éléments du maillage ont été implémentés. Il est ainsi possible de faire :
for (int i = 0; i < mesh.nb_nodes(); i++)
ofile << *mesh.node(i) << endl;
Pour évaluer la fonction f sur chaque noeud du maillage, il faut passer les coordonnées du noeud en argument de Evaluator :
for (int i = 0; i < mesh.nb_nodes(); i++)
{
Node *n = mesh.node(i);
ofile << eval_f(n->x(), n->y()) << std::endl;
}
Tests
Dans tests/part_2.cpp, deux Evaluator ont été créés pour tester l'évaluation des fonctions de l'énoncé :
EvaluatorExpr eval_f1([](double x, double y)
{ return x * x + y * y; });
EvaluatorExpr eval_f2([](double x, double y)
{ return pow(x - 0.5, 2) + pow(y - 0.5, 2); });
export_vtk(mesh_M2, eval_f1, "../output/mesh_M2_eval");
export_vtk(mesh_perforated, eval_f2, "../output/mesh_perforated_eval");
Deux fichiers .vtk sont générés en sortie et sont disponibles dans le dossier output du projet. Ces fichiers peuvent être visualisés avec Paraview.
Intégration numérique
La méthode double Mesh::integral(int quad_order, Evaluator const &eval_f) const permet de calculer une intégrale sur le maillage en sommant les intégrales sur les triangles du maillage.
Cette méthode prend en argument l'ordre de quadrature quad_order et un évaluateur de fonction eval_f.
Une méthode permettant de calculer l'intégrale sur un triangle est également implémentée double Element::integral(int quad_order, Evaluator const &eval_f, Node **nodes) const.
Cette méthode prend en argument l'ordre de quadrature quad_order, un évaluateur de fonction eval_f et un pointeur vers le tableau des noeuds du maillage Node **nodes.
Accès aux noeuds
Un pointeur vers le tableau des noeuds du maillage Node **nodes est nécéssaire pour accéder aux coordonnées des noeuds.
La fonction d'intégration sur un élément calcule ainsi l'intégrale sur l'élément en utilisant les différentes formules de quadratures fournies par l'énoncé.
Tests
Les fonctions tests définies précédemment permettent de vérifier que les résultats calculés sont corrects.
Nous allons traiter différents examples dans le but de vérifier le bon fonctionnement de la méthode Mesh::integral.
Calculons l'intégrale suivante sur le maillage mesh_M0 :
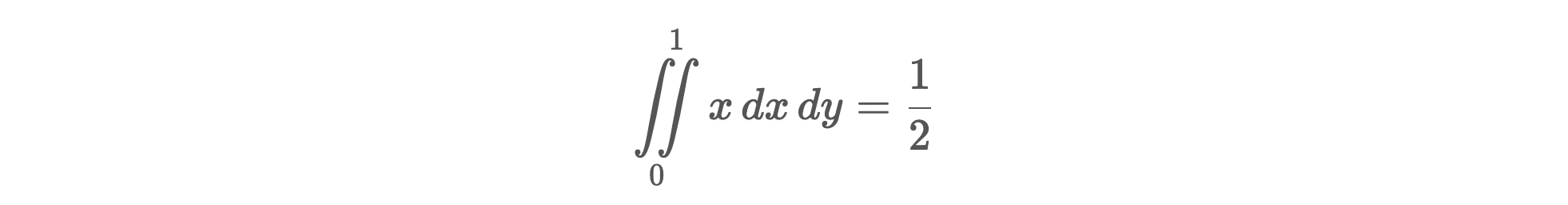
EvaluatorExpr eval_fx1([](double x, double y)
{ return pow(x, 1); });
double exact1 = 1. / 2.;
std::cout << "test passed pow(x, 1) (ord 1): " << std::setprecision(15) << std::boolalpha << check_double_equal(exact1 - mesh_M0.integral(1, eval_fx1), 0., tol) << std::endl;
std::cout << "test passed pow(x, 1) (ord 2): " << std::setprecision(15) << std::boolalpha << check_double_equal(exact1 - mesh_M0.integral(2, eval_fx1), 0., tol) << std::endl;
std::cout << "test passed pow(x, 1) (ord 3): " << std::setprecision(15) << std::boolalpha << check_double_equal(exact1 - mesh_M0.integral(3, eval_fx1), 0., tol) << std::endl;
Comme attendu, l'erreur est nulle pour les ordres de quadrature 1, 2 et 3.
Calculons l'intégrale suivante sur le maillage mesh_M0 :
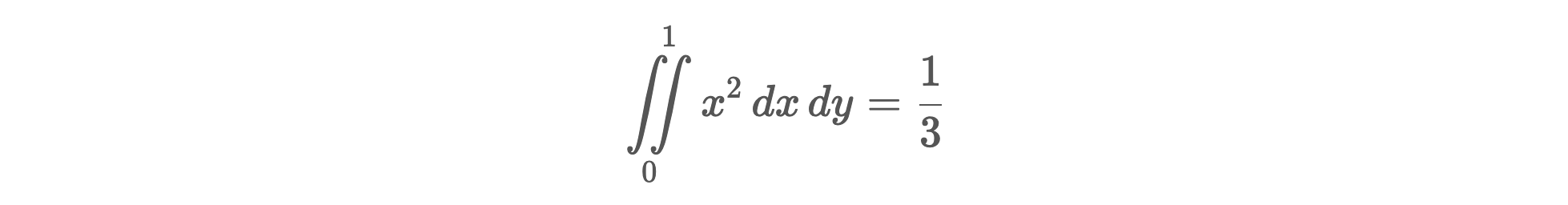
EvaluatorExpr eval_fx2([](double x, double y)
{ return pow(x, 2); });
double exact2 = 1. / 3.;
std::cout << "test passed pow(x, 2) (ord 1): " << std::setprecision(15) << std::boolalpha << check_double_not_equal(exact2 - mesh_M0.integral(1, eval_fx2), 0., tol) << std::endl;
std::cout << "test passed pow(x, 2) (ord 2): " << std::setprecision(15) << std::boolalpha << check_double_equal(exact2 - mesh_M0.integral(2, eval_fx2), 0., tol) << std::endl;
std::cout << "test passed pow(x, 2) (ord 3): " << std::setprecision(15) << std::boolalpha << check_double_equal(exact2 - mesh_M0.integral(3, eval_fx2), 0., tol) << std::endl;
Comme attendu, l'erreur est nulle pour les ordres de quadrature 2 et 3 et le résultat est approximatif pour l'ordre 1.
Calculons l'intégrale suivante sur le maillage mesh_M0 :
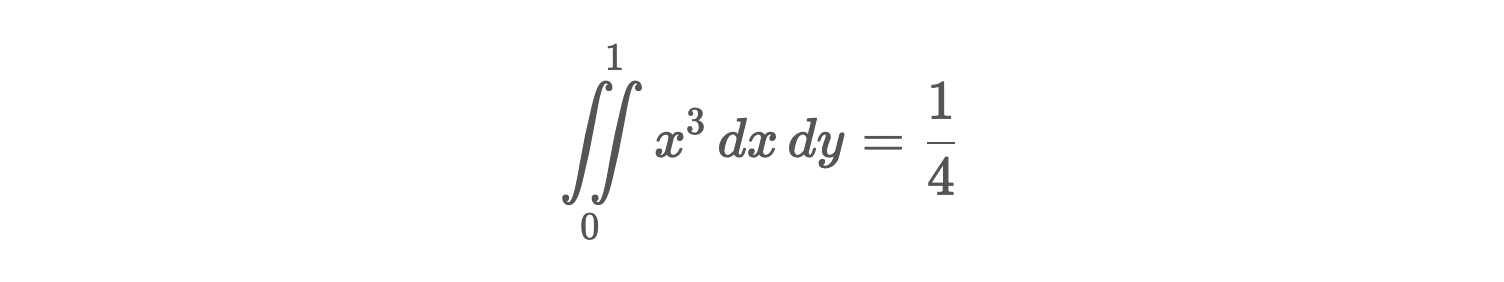
EvaluatorExpr eval_fx3([](double x, double y)
{ return pow(x, 3); });
double exact3 = 1. / 4.;
std::cout << "test passed pow(x, 3) (ord 1): " << std::setprecision(15) << std::boolalpha << check_double_not_equal(exact3 - mesh_M0.integral(1, eval_fx3), 0., tol) << std::endl;
std::cout << "test passed pow(x, 3) (ord 2): " << std::setprecision(15) << std::boolalpha << check_double_not_equal(exact3 - mesh_M0.integral(2, eval_fx3), 0., tol) << std::endl;
std::cout << "test passed pow(x, 3) (ord 3): " << std::setprecision(15) << std::boolalpha << check_double_equal(exact3 - mesh_M0.integral(3, eval_fx3), 0., tol) << std::endl;
Comme attendu, l'erreur est nulle pour l'ordre de quadrature 3 et le résultat est approximatif pour les ordres 1 et 2.
Calculons l'intégrale suivante sur le maillage mesh_M0 :
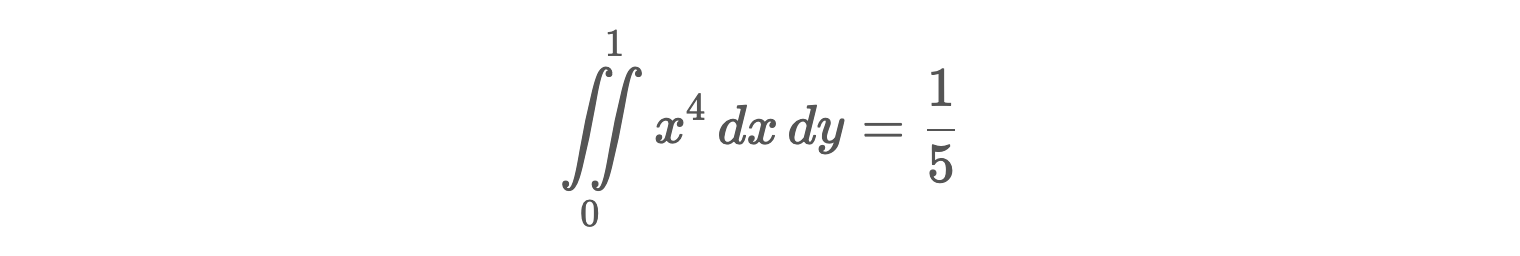
EvaluatorExpr eval_fx4([](double x, double y)
{ return pow(x, 4); });
double exact4 = 1. / 5.;
std::cout << "test passed pow(x, 4) (ord 1): " << std::setprecision(15) << std::boolalpha << check_double_not_equal(exact4 - mesh_M0.integral(1, eval_fx4), 0., tol) << std::endl;
std::cout << "test passed pow(x, 4) (ord 2): " << std::setprecision(15) << std::boolalpha << check_double_not_equal(exact4 - mesh_M0.integral(2, eval_fx4), 0., tol) << std::endl;
std::cout << "test passed pow(x, 4) (ord 3): " << std::setprecision(15) << std::boolalpha << check_double_not_equal(exact4 - mesh_M0.integral(3, eval_fx4), 0., tol) << std::endl;
Comme attendu, le résultat est approximatif pour les ordres 1, 2 et 3.
Si l'on calcule maintenant une intégrale non polynomiale sur les maillages en fonction du raffinement, on constate que plus le maillage est fin, plus l'erreur est faible.
Calculons l'intégrale suivante sur les maillages mesh_M0, mesh_M1 et mesh_M2 :
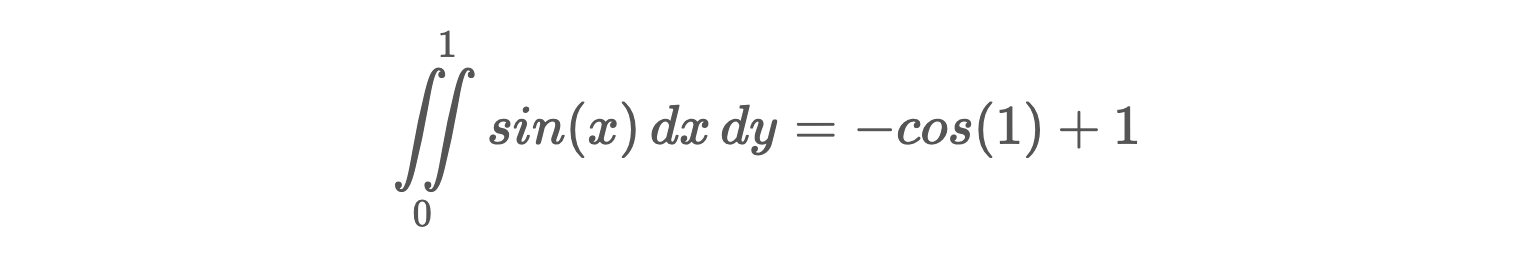
EvaluatorExpr eval_fsin([](double x, double y)
{ return sin(x); });
double exact5 = -cos(1.) + 1.;
std::cout << "error integral sin(x) (ord 1 ; mesh_M0): " << std::setprecision(15) << exact5 - mesh_M0.integral(1, eval_fsin) << std::endl;
std::cout << "error integral sin(x) (ord 2 ; mesh_M0): " << std::setprecision(15) << exact5 - mesh_M0.integral(2, eval_fsin) << std::endl;
std::cout << "error integral sin(x) (ord 3 ; mesh_M0): " << std::setprecision(15) << exact5 - mesh_M0.integral(3, eval_fsin) << std::endl;
std::cout << "----------------------------------------" << std::endl;
std::cout << "error integral sin(x) (ord 1 ; mesh_M1): " << std::setprecision(15) << exact5 - mesh_M1.integral(1, eval_fsin) << std::endl;
std::cout << "error integral sin(x) (ord 2 ; mesh_M1): " << std::setprecision(15) << exact5 - mesh_M1.integral(2, eval_fsin) << std::endl;
std::cout << "error integral sin(x) (ord 3 ; mesh_M1): " << std::setprecision(15) << exact5 - mesh_M1.integral(3, eval_fsin) << std::endl;
std::cout << "----------------------------------------" << std::endl;
std::cout << "error integral sin(x) (ord 1 ; mesh_M2): " << std::setprecision(15) << exact5 - mesh_M2.integral(1, eval_fsin) << std::endl;
std::cout << "error integral sin(x) (ord 2 ; mesh_M2): " << std::setprecision(15) << exact5 - mesh_M2.integral(2, eval_fsin) << std::endl;
std::cout << "error integral sin(x) (ord 3 ; mesh_M2): " << std::setprecision(15) << exact5 - mesh_M2.integral(3, eval_fsin) << std::endl;
Ce qui donne :
----------------------------------------
error integral sin(x) (ord 1 ; mesh_M0): -1.5240804644101e-05
error integral sin(x) (ord 2 ; mesh_M0): 1.17365450691409e-10
error integral sin(x) (ord 3 ; mesh_M0): 1.22962640070057e-10
----------------------------------------
error integral sin(x) (ord 1 ; mesh_M1): -3.82097363854639e-06
error integral sin(x) (ord 2 ; mesh_M1): 7.14239778432102e-12
error integral sin(x) (ord 3 ; mesh_M1): 7.65359997600967e-12
----------------------------------------
error integral sin(x) (ord 1 ; mesh_M2): -9.56634027104997e-07
error integral sin(x) (ord 2 ; mesh_M2): 4.24493773465429e-13
error integral sin(x) (ord 3 ; mesh_M2): 4.82947015711943e-13
----------------------------------------